2020年公务员考试行测练习:数学运算
发布时间:2019-07-02 16:04:10 来源:灵鹏教育
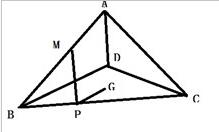
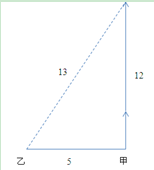
1.甲地在乙地正东5公里,某天早上7点30分,小赵从乙地出发,以每小时15公里的速度骑车前往甲地找小张,但在小赵出发的同时,小张也出发以每小时9公里的速度向正北方向跑步锻炼。小赵到甲地后立刻沿校长跑步的路径以每小时12公里的速度追小张,追上小张后,两人以每小时10公里的速度从相遇点沿直线距离返回乙地。问返回乙地时的时间是几点?
A.10点08分
B.10点14分
C.10点20分
D.10点02分
2.火车通过560米长的隧道用20秒,如果速度增加20%,通过1200米的隧道用30秒。火车的长度是多少米?( )
A.220
B.240
C.250
D.260
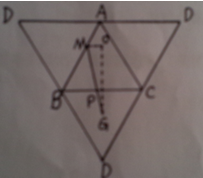
3.如图,A-BCD是棱长为3的正四面体,M是棱上的一点,且MB=2MA ,G是三角形BCD的重心,动点P在棱BC上,则PM+PG的最小值

A.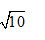 B.
B.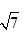 C
C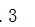 D.
D.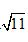
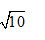 B.
B.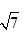 C
C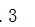 D.
D.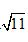
4.某制衣厂接受一批服装订货任务,按计划天数进行生产,如果每天平均生产20套服装,就比订货任务少生产100套;如果每天生产23套服装,就可超过订货任务20套。那么,这批服装的订货任务是多少套?( )
A.760
B.1120
C.900
D.850
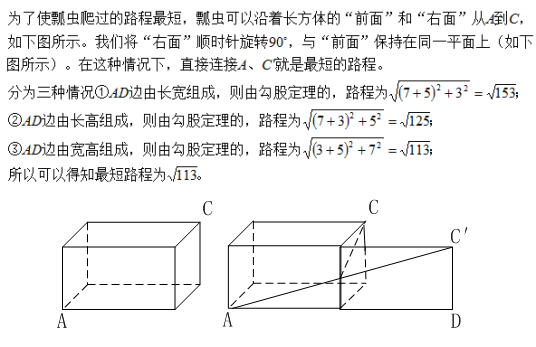
5.一个长7厘米、宽5厘米、高3厘米的长方体盒子。一只瓢虫从盒子的任意一个顶点,爬到与设定点在同一体对角线的另一个顶点,则所有情形的爬行路线的最小值是( )。
A.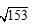 B.
B. C.
C.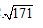 D.
D.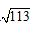
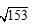 B.
B. C.
C.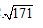 D.
D.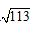
答案与解析
1.答案: A
解析:如下图,小赵从乙地到达甲地需要的时间为5/15=1/3小时,此时小张从甲地出发走了9×1/3=3公里,设小赵从甲地追上小张需要的时间为t,则3=(12-9)t,t=1小时,此时小赵从甲地走了12公里,故小赵追上小张时俩人距离甲地12公里。在直角三角形中,俩人返回时走的距离为,需要时间为13/10=1.3小时,故小赵总共走的时间为(1/3+1+1.3)小时,共2小时38分钟,此时应该是10点08分,故本题答案为A选项。

2.答案: B
解析:设火车长度为s,速度为v,根据题意可得:s+560=20v,s+1200=30×1.2v,解得:s=240,v=40。因此正确答案为B。
3.答案: B
解析:把四面体展开成一个正三角形,则M点在棱AB的三分之一处,G是△BCD的重心,则当点P在线段MG上时,PM+PG=MG值最小。构造Rt△OMG,点O在线段AG上,根据相似比可求解出,则根据勾股定理可得,故本题的正确答案为B。

4.答案: C
解析1:假设订货任务为x套,计划天数为y天,则可得:20y+100=x,23y-20=x,解得x=900,y=40。故正确答案为C。
解析2:根据题意订货的套数加上20可以被23整除,观察选项,只有C符合。
5.答案: D
解析:
解析:







